logoChat01.ai

Uma cobertura em treliça possui essa configuração ...

Criado em: 12 de maio de 2025

Respondido usando O3 por Chat01

Pergunta

07b2bb8475165a85688f675888a96101.jpeg07b2bb8475165a85688f675888a96101.jpeg

Uma cobertura em treliça possui essa configuração mostrada abaixo. Determine seu grau de estaticidade:

Python

python
from PIL import Image
import matplotlib.pyplot as plt

img = Image.open('/mnt/data/07b2bb8475165a85688f675888a96101.jpeg')
plt.imshow(img); plt.axis('off')

(-0.5, 3031.5, 895.5, -0.5)

Python

python
plt.figure(figsize=(4,2))
plt.imshow(img.crop((900,0,1589,498))); plt.axis('off')

(-0.5, 688.5, 497.5, -0.5)

Python

python
plt.figure(figsize=(6,2))
plt.imshow(img.crop((700,0,1589,498))); plt.axis('off')

(-0.5, 888.5, 497.5, -0.5)

Python

python
plt.figure(figsize=(6,2))
plt.imshow(img.crop((0,200,1589,498))); plt.axis('off')

(-0.5, 1588.5, 297.5, -0.5)

Python

python
plt.figure(figsize=(6,2))
plt.imshow(img.crop((0,0,800,498))); plt.axis('off')

(-0.5, 799.5, 497.5, -0.5)

Python

python
plt.figure(figsize=(6,4))
plt.imshow(img.crop((0,200,800,700))); plt.axis('off')

(-0.5, 799.5, 499.5, -0.5)

Python

python
plt.figure(figsize=(6,4))
plt.imshow(img.crop((0,200,800,700))); plt.axis('off')

(-0.5, 799.5, 499.5, -0.5)

(-0.5, 799.5, 499.5, -0.5)

text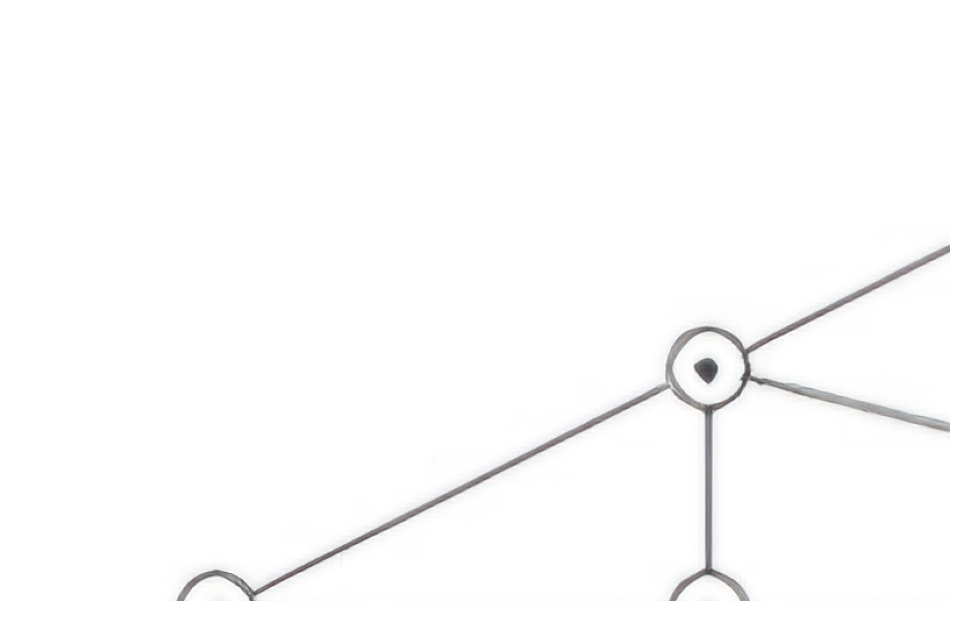

![](https://files.openai01.net/python-generations/files/file-2cHuqzXnveUuwPebD9UqjD)

Python

python
plt.figure(figsize=(6,4))
plt.imshow(img.crop((0,550,800,1100))); plt.axis('off')

(-0.5, 799.5, 549.5, -0.5)

Python

python
plt.figure(figsize=(6,4))
plt.imshow(img.crop((600,550,1400,1100))); plt.axis('off')

(-0.5, 799.5, 549.5, -0.5)

Python

python
print(img.size)

Python

python
plt.figure(figsize=(6,4))
plt.imshow(img.crop((0,400,900,896))); plt.axis('off')

(-0.5, 899.5, 495.5, -0.5)

Python

python
plt.figure(figsize=(6,4))
plt.imshow(img.crop((600,0,1350,600))); plt.axis('off')

(-0.5, 749.5, 599.5, -0.5)

Python

python
plt.figure(figsize=(6,4))
plt.imshow(img.crop((900,200,1500,800))); plt.axis('off')

(-0.5, 599.5, 599.5, -0.5)

Python

python
plt.figure(figsize=(6,4))
plt.imshow(img.crop((1400,400,2300,896))); plt.axis('off')

(-0.5, 899.5, 495.5, -0.5)

Python

python
plt.figure(figsize=(6,4))
plt.imshow(img.crop((2300,400,3032,896))); plt.axis('off')

(-0.5, 731.5, 495.5, -0.5)

Python

python
plt.figure(figsize=(6,4))
plt.imshow(img.crop((1800,300,2300,896))); plt.axis('off')

(-0.5, 499.5, 595.5, -0.5)

Python

python
plt.figure(figsize=(6,4))
plt.imshow(img.crop((0,300,500,896))); plt.axis('off')

(-0.5, 499.5, 595.5, -0.5)

Python

python
plt.figure(figsize=(6,4))
plt.imshow(img.crop((300,200,800,600))); plt.axis('off')

(-0.5, 499.5, 399.5, -0.5)

Python

python
plt.figure(figsize=(6,4))
plt.imshow(img.crop((300,350,800,896))); plt.axis('off')

(-0.5, 499.5, 545.5, -0.5)

Python

python
plt.figure(figsize=(6,4))
plt.imshow(img.crop((800,0,1200,600))); plt.axis('off')

(-0.5, 399.5, 599.5, -0.5)

Python

python
plt.figure(figsize=(10,3))
plt.imshow(img); plt.axis('off')

(-0.5, 3031.5, 895.5, -0.5)

Python

python
plt.figure(figsize=(6,4))
plt.imshow(img.crop((0,300,600,800))); plt.axis('off')

(-0.5, 599.5, 499.5, -0.5)

Python

python
plt.figure(figsize=(10,4))
plt.imshow(img.crop((0,200,1500,900))); plt.axis('off')

(-0.5, 1499.5, 699.5, -0.5)

Python

python
plt.figure(figsize=(10,4))
plt.imshow(img.crop((0,200,1500,900))); plt.axis('off')

(-0.5, 1499.5, 699.5, -0.5)

(-0.5, 1499.5, 699.5, -0.5)

text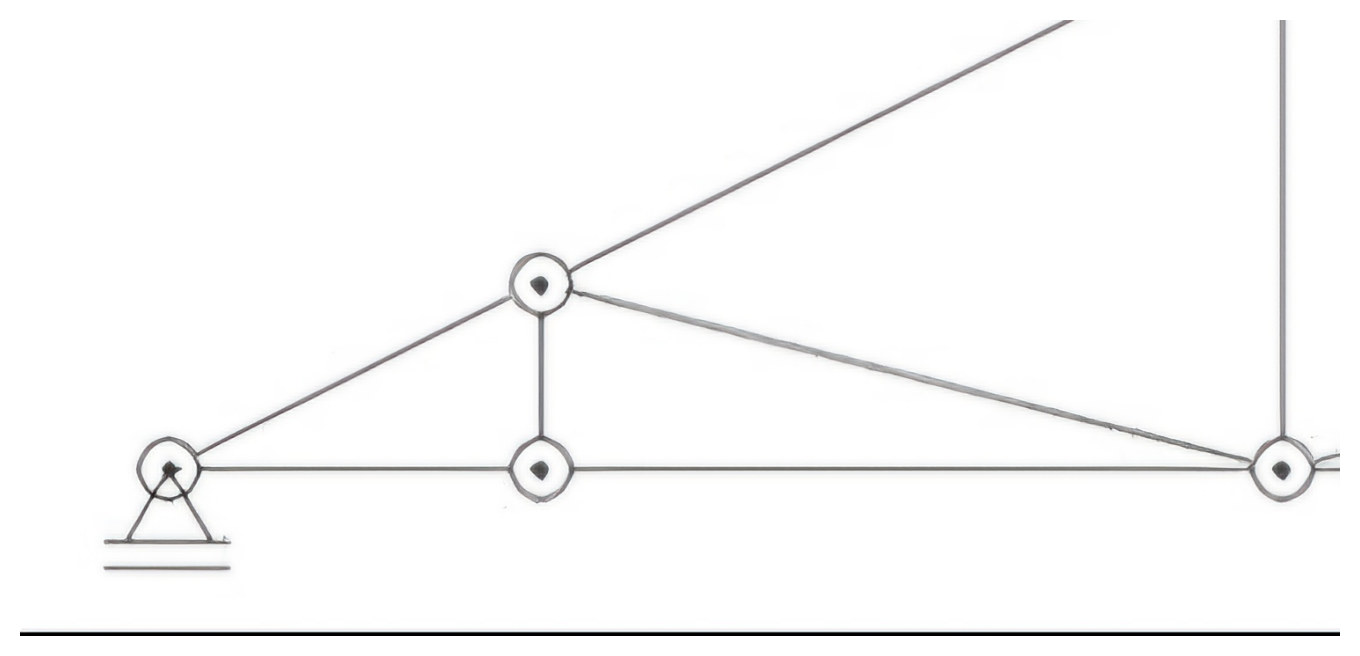

![](https://files.openai01.net/python-generations/files/file-AoLMuhjXPvZbVYqrF5T1iN)

Python

python
plt.figure(figsize=(10,4))
plt.imshow(img.crop((800,0,1600,900))); plt.axis('off')

(-0.5, 799.5, 899.5, -0.5)

Python

python
plt.figure(figsize=(6,4))
plt.imshow(img.crop((1200,200,1800,800))); plt.axis('off')

(-0.5, 599.5, 599.5, -0.5)

Python

python
plt.figure(figsize=(6,4))
plt.imshow(img.crop((1800,200,2700,800))); plt.axis('off')

(-0.5, 899.5, 599.5, -0.5)

Python

python
plt.figure(figsize=(6,4))
plt.imshow(img.crop((2200,200,3032,800))); plt.axis('off')

(-0.5, 831.5, 599.5, -0.5)

Python

python
plt.figure(figsize=(6,4))
plt.imshow(img.crop((2000,500,3032,896))); plt.axis('off')

(-0.5, 1031.5, 395.5, -0.5)

Python

python
plt.figure(figsize=(6,4))
plt.imshow(img.crop((0,400,800,800))); plt.axis('off')

(-0.5, 799.5, 399.5, -0.5)

Python

python
plt.figure(figsize=(6,4))
plt.imshow(img.crop((0,400,800,800))); plt.axis('off')

(-0.5, 799.5, 399.5, -0.5)

(-0.5, 799.5, 399.5, -0.5)

text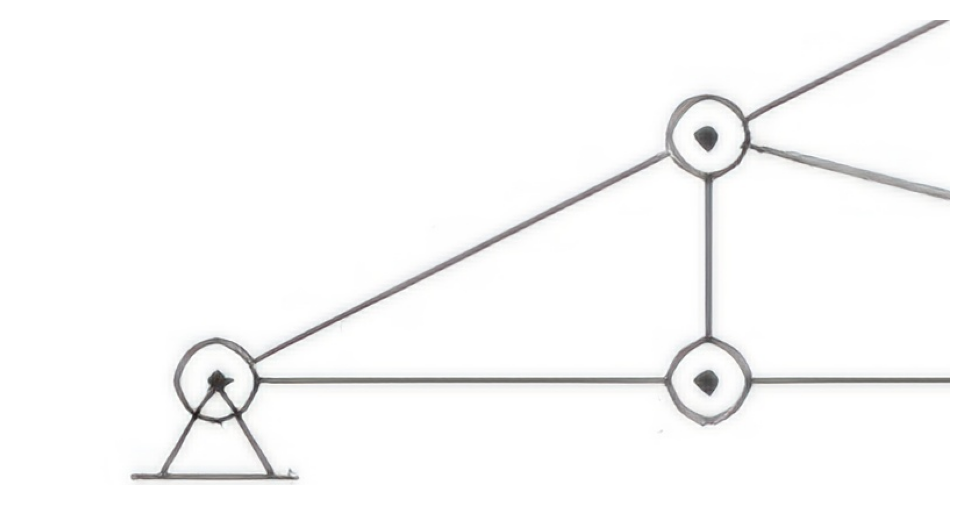

![](https://files.openai01.net/python-generations/files/file-F5aaQm3mbtkjhxkLA2j9Uj)

Python

python
plt.figure(figsize=(4,4))
plt.imshow(img.crop((200,500,500,800))); plt.axis('off')

(-0.5, 299.5, 299.5, -0.5)

Python

python
plt.figure(figsize=(4,4))
plt.imshow(img.crop((200,400,800,550))); plt.axis('off')

(-0.5, 599.5, 149.5, -0.5)

Python

python
plt.figure(figsize=(10,3))
plt.imshow(img); plt.show()

Python

python
plt.figure(figsize=(6,4))
plt.imshow(img.crop((0,200,900,550))); plt.axis('off')

(-0.5, 899.5, 349.5, -0.5)

Python

python
plt.figure(figsize=(6,4))
plt.imshow(img.crop((0,350,700,800))); plt.axis('off')

(-0.5, 699.5, 449.5, -0.5)

Python

python
plt.figure(figsize=(6,4))
plt.imshow(img.crop((2200,650,3032,850))); plt.axis('off')

(-0.5, 831.5, 199.5, -0.5)

Python

python
plt.figure(figsize=(4,4))
plt.imshow(img.crop((2300,650,2600,850))); plt.axis('off')

(-0.5, 299.5, 199.5, -0.5)

Python

python
plt.figure(figsize=(4,4))
plt.imshow(img.crop((2300,650,2600,850))); plt.axis('off')

(-0.5, 299.5, 199.5, -0.5)

(-0.5, 299.5, 199.5, -0.5)

text

![](https://files.openai01.net/python-generations/files/file-8ZZwr5v4LLqRX6ZvdJEpdJ)

Python

python
plt.figure(figsize=(4,4))
plt.imshow(img.crop((2300,650,2600,850))); plt.axis('off')

(-0.5, 299.5, 199.5, -0.5)

(-0.5, 299.5, 199.5, -0.5)

text

![](https://files.openai01.net/python-generations/files/file-8ZZwr5v4LLqRX6ZvdJEpdJ)



(-0.5, 299.5, 199.5, -0.5)

Python

python
plt.figure(figsize=(4,4))
plt.imshow(img.crop((2500,650,3032,850))); plt.axis('off')

(-0.5, 531.5, 199.5, -0.5)

Python

python
plt.figure(figsize=(4,4))
plt.imshow(img.crop((2500,650,3032,850))); plt.axis('off')

(-0.5, 531.5, 199.5, -0.5)

(-0.5, 531.5, 199.5, -0.5)

text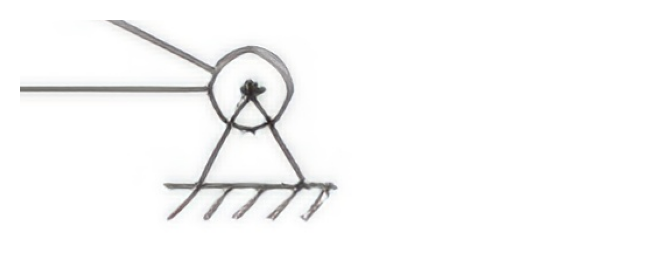

![](https://files.openai01.net/python-generations/files/file-S659P8dbMtbxkmCYrVoNwu)

Pensamento

Confirming bottom chord and member count

There's a horizontal line leaving the bottom intermediate node heading right, but it doesn't quite reach the support—though that might be in the next crop. There’s another line heading directly into the support node, confirming that the bottom chord segment (4-5) is present. The total is still 13 members, with 8 joints (supporting nodes A, B, C, D, F, G, H, and J). Plus, a quick check of the formula confirms everything's working out for a determinate truss.

Thought for 7m 5s

Resposta

Passo‑a‑passo do balanço de incógnitas

QuantidadeSímboloComo foi obtidoValor
Nós (j)jj5 nós na corda inferior (apoios A e J + 3 nós intermediários) + 3 nós na corda superior (2 intermediários + o ápice)8
Barras (m)mm4 da corda inferior (A‑B, B‑F, F‑H, H‑J)<br>3 montantes verticais (B‑C, F‑D, H‑G)<br>2 da corda superior (C‑D, D‑G)<br>4 diagonais (A‑C, C‑F, F‑G, G‑J)13
Reacções de apoio (r)rrPino em A: 2 · Roda em J: 13

Grau de estaticidade

Para treliças planas usa‑se

G=m+r−2 j\boxed{G = m + r - 2\,j} G=13+3−2(8)=16−16=0G = 13 + 3 - 2(8) = 16 - 16 = 0

Conclusão

  • G=0G = 0  → treliça isostática
    (nem hiperestática nem hipostática; todas as forças internas e reacções podem ser determinadas apenas com as equações de equilíbrio).

Observação extra: o critério interno m=2j−3m = 2j - 3 também é satisfeito (13 = 2·8 – 3), confirmando que a geometria está devidamente triangulada e não há mecanismos.

Compartilhar esta Q&A