# U366413 六边形（hexagon） ## 题目描述一个六边形的图如下所示。 ![]...

Question

U366413 六边形（hexagon）

题目描述

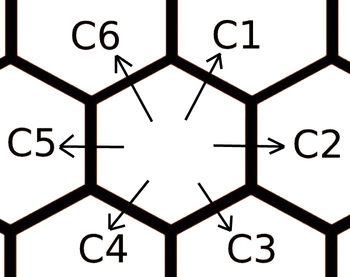
一个六边形的图如下所示。

小a现在正在点 $(0,0)$ ，他希望自己能够到达给定的坐标 $(x,y)$ ，它可以一步到达六边形的六个邻居的任何一个，但是到达不同的邻居有不同的花费，这个花费仅仅跟你移动的方向有关。这个花费在输入中按照 $c_1,c_2,c_3,c_4,c_5,c_6$ 的顺序给出。

现在请你告诉小a从 $(0,0)$ 到 $(x,y)$ 的最小花费。

输入格式

第一行一个正整数 $T$ 表示数据组数。

对于每一组数据，第一行两个整数 $x,y$ 。

接下来的一行包含 $6$ 个整数， $c_1,c_2,c_3,c_4,c_5,c_6$ 。

输出格式

对于每一组数据，一行表示最小花费。

输入输出样例 #1

输入 #1

text
1
-3 1
1 3 5 7 9 11

输出 #1

说明/提示

解释#1

对于第一组数据：

$5+5+5+3=18$

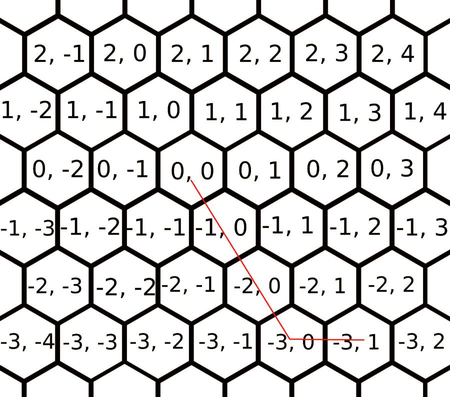
数据范围

对于 $20\%$ 的数据，保证 $-2 \leq x,y \leq 2, \ 1\leq T \leq 10^4$ 。

对于另外 $20\%$ 的数据，保证 $-100 \leq x,y \leq 100, \ 1\leq T \leq 100$ 。

对于 $100\%$ 的数据，保证 $-10^9 \leq x,y \leq 10^9, \ 1\leq c_i \leq 10^9 \ 1\leq T \leq 10^4$ 。 uSING c++ TO SOLVE

Answer 1

下面给出一种通用、稳妥且可过满数据的做法与 C++ 实现。

思路（要点）

六个方向按题图顺时针编号：
c1： $(+1,0)$ （右上），c2： $(0,+1)$ （正右），c3： $(-1,+1)$ （右下），
c4： $(-1,0)$ （左下），c5： $(0,-1)$ （正左），c6： $(+1,-1)$ （左上）。
先做“费用松弛”：
对每个方向 $i$ ，用相邻两方向 $i-1,i+1$ 的组合替代它：
$c_i=\min\{c_i,\ c_{i-1}+c_{i+1}\}$ （下标环状）。多做几轮直至稳定。这样保证“走弯路”不会比“直走”更便宜。
平面被这 6 个方向分成 6 个扇区。目标点 $(x,y)$ 必落在某个由相邻两方向张成的扇区内。
在该扇区内，只用这相邻两种步子，就能线性表示目标且最优。解出非负系数即可：

设六方向向量依次为
$v_1=(1,0), v_2=(0,1), v_3=(-1,1), v_4=(-1,0), v_5=(0,-1), v_6=(1,-1)$ 。
- 扇区 $v_1\sim v_2$ （ $x\ge0,y\ge0$ ）： $(x,y)=x\,v_1+y\,v_2$ ，费用 $x\,c_1+y\,c_2$ 。
- 扇区 $v_2\sim v_3$ （ $x\le0,y\ge0,x+y\ge0$ ）：
  $(x,y)=(x+y)\,v_2+(-x)\,v_3$ ，费用 $(x+y)c_2+(-x)c_3$ 。
- 扇区 $v_3\sim v_4$ （ $x\le0,y\ge0,x+y\le0$ ）：
  $(x,y)=y\,v_3+(-x-y)\,v_4$ ，费用 $y\,c_3+(-x-y)c_4$ 。
- 扇区 $v_4\sim v_5$ （ $x\le0,y\le0$ ）： $(x,y)=(-x)\,v_4+(-y)\,v_5$ ，费用 $(-x)c_4+(-y)c_5$ 。
- 扇区 $v_5\sim v_6$ （ $x\ge0,y\le0,x+y\le0$ ）：
  $(x,y)=(-x-y)\,v_5+x\,v_6$ ，费用 $(-x-y)c_5+x\,c_6$ 。
- 扇区 $v_6\sim v_1$ （ $x\ge0,y\le0,x+y\ge0$ ）：
  $(x,y)=(-y)\,v_6+(x+y)\,v_1$ ，费用 $(-y)c_6+(x+y)c_1$ 。
上述各式系数均为非负（由扇区条件保证），因此直接得到最小费用。

代码（C++17）

cpp
#include <bits/stdc++.h>
using namespace std;
using int64 = long long;

int main() {
    ios::sync_with_stdio(false);
    cin.tie(nullptr);
    int T; 
    if(!(cin >> T)) return 0;
    while (T--) {
        long long x, y;
        cin >> x >> y;
        // c[1..6]
        long long c[7];
        for (int i = 1; i <= 6; ++i) cin >> c[i];

        // 费用松弛：邻边替代，循环几次到稳定
        for (int rep = 0; rep < 4; ++rep) {
            for (int i = 1; i <= 6; ++i) {
                int L = (i == 1 ? 6 : i - 1);
                int R = (i == 6 ? 1 : i + 1);
                c[i] = min(c[i], c[L] + c[R]);
            }
        }

        long long ans = 0;
        if (x >= 0 && y >= 0) {
            // sector v1~v2
            ans = x * c[1] + y * c[2];
        } else if (x <= 0 && y <= 0) {
            // sector v4~v5
            ans = (-x) * c[4] + (-y) * c[5];
        } else if (x <= 0 && y >= 0) {
            if (x + y >= 0) {
                // sector v2~v3
                ans = (x + y) * c[2] + (-x) * c[3];
            } else {
                // sector v3~v4
                ans = y * c[3] + (-x - y) * c[4];
            }
        } else { // x >= 0 && y <= 0
            if (x + y <= 0) {
                // sector v5~v6
                ans = (-x - y) * c[5] + x * c[6];
            } else {
                // sector v6~v1
                ans = (-y) * c[6] + (x + y) * c[1];
            }
        }
        cout << ans << "\n";
    }
    return 0;
}

复杂度：每组常数时间 $O(1)$ ，可轻松应对 $|x|,|y|\le 10^9,\ T\le 10^4$ 。

# U366413 六边形（hexagon） ## 题目描述一个六边形的图如下所示。 ![]...

问题

U366413 六边形（hexagon）

题目描述

输入格式

输出格式

输入输出样例 #1

输入 #1

输出 #1

说明/提示

Python

Python

Python

Python

Python

Python

思考

Testing mappings and sector approach

Clarifying sector mapping

Final C++ Code Approach

回答

思路（要点）

代码（C++17）

分享这个问答